C# to Go: a beginner's journey (part 3)

The next step for GoRender is an easy choice. I want to write the raycaster, a critical part of turning voxel objects into pixel sprites. The C# version involves a lot of vector mathematics, so implementing it in Go will touch on yet another new area.
At the end of Part 2, I had the following output:

The Transrender equivalent is this:

There's a lot of palette handling and shading in there, and to start with I only want to know that my raycaster can successfully cast rays to a voxel object and return something the correct shape - so to start with, I'll be happy if my output looks something like this:
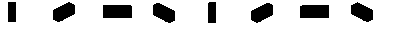
Transrender's raycast renderer is one of its more readable parts, but you can still see the vestiges of too much "iterate" and not enough "stabilise" in those long methods, module-level variables and the mixing up of the sun vector and rendering vector initialisation.
It's a classic ray caster, and works like this:
- For each pixel in the output image, set up a ray with a start position and increment.
- Increment the ray until it collides with a voxel or is outside of the voxel grid and facing away from it.
- If there was a collision, set the pixel of the output image accordingly.
Setting up each ray is based on a camera plane, which is where most of the complex maths comes in. Identifying the plane is done thus:
- Get the direction rendering rays will take using simple trigonometry, based on the current render angle.
- Calculate both the normal of the render direction, and the direction with no height (z) component.
- Use these to create a "plane normal". The camera plane is described by this and the render normal. (This is actually a pointless calculation - the plane normal is always [0,0,1] with Transrender's settings)
- Scale the unit-length plane vectors by the size of voxel object.
- Set the initial viewpoint to 100 render steps away from the assumed centre of the object.
- Calculate the corners of the plane.
The ray starting points are then linearly interpolated across the viewing plane.
This gives us some good starting points to build up the raycast renderer. I'm going to begin with getting the ray direction.
Vectors
Getting the ray direction throws up the first question: what should the return type be? In C# we use the framework's Vector3 type. Go's library doesn't have a native version of this - I could pull in a library which features its own Vector3 equivalent like geo (https://github.com/golang/geo) but it's a bit heavyweight and still missing some of the functions I use like linear interpolation.
What vector operations do I use? In the renderer, it's these:
- Add
- Subtract
- Multiply by constant
- Multiply by vector
- Normalise
- Cross product
- Dot product (in shader)
- Lerp
- Get zero vector
This feels a small enough scope to write my own small library. I'll also add methods to get the unit X,Y and Z vectors as that will be useful for testing.
This is a simple library so I feel happy to write all the tests in one hit and then implement all the methods afterward. The test code looks like this:
package vector3
import "testing"
func testVector(expected Vector3, vector Vector3, t *testing.T) {
if vector != expected {
t.Errorf("Expected %v, got %v", expected, vector)
}
}
func TestZero(t *testing.T) {
testVector(Vector3{0, 0, 0}, Zero(), t)
}
func TestUnitX(t *testing.T) {
testVector(Vector3{1, 0, 0}, UnitX(), t)
}
func TestUnitY(t *testing.T) {
testVector(Vector3{0, 1, 0}, UnitY(), t)
}
func TestUnitZ(t *testing.T) {
testVector(Vector3{0, 0, 1}, UnitZ(), t)
}
func TestVector3_Add(t *testing.T) {
testVector(Vector3{1, 1, 0}, UnitX().Add(UnitY()), t)
}
func TestVector3_Subtract(t *testing.T) {
testVector(Vector3{1, -1, 0}, UnitX().Subtract(UnitY()), t)
}
func TestVector3_MultiplyByConstant(t *testing.T) {
testVector(Vector3{1.5, 0, 0}, UnitX().MultiplyByConstant(1.5), t)
}
func TestVector3_MultiplyByVector(t *testing.T) {
testVector(Vector3{1.5, 0, 0}, UnitX().MultiplyByVector(Vector3{1.5, 0, 0}), t)
}
func TestVector3_Normalise(t *testing.T) {
testVector(Vector3{1, 0, 0}, Vector3{2, 0, 0}.Normalise(), t)
}
func TestVector3_Cross(t *testing.T) {
testVector(UnitZ(), UnitX().Cross(UnitY()), t)
}
func TestVector3_Dot(t *testing.T) {
val := Vector3{1, 2, 1}.Dot(Vector3{2, 1, 4})
expected := 8.0
if val != expected {
t.Errorf("Dot product expected %f got %f", expected, val)
}
}
func TestVector3_Lerp(t *testing.T) {
testVector(Vector3{0.75, 0.25, 0}, UnitX().Lerp(UnitY(), 0.25), t)
}
Note that I'm expecting to be able to call methods on a Vector3 to keep code concise and readable - but this isn't an object-oriented language. Go's means of doing this is declaring a method on the type:
func (a Vector3) Add(b Vector3) Vector3 {
}Right now I have a bunch of failing tests, so I'll go through and implement my simple vector library.
package vector3
import "math"
type Vector3 struct {
X, Y, Z float64
}
func Zero() Vector3 {
return Vector3{0,0,0}
}
func UnitX() Vector3 {
return Vector3{1,0,0}
}
func UnitY() Vector3 {
return Vector3{0,1,0}
}
func UnitZ() Vector3 {
return Vector3{0,0,1}
}
func (a Vector3) Add(b Vector3) Vector3 {
return Vector3{a.X + b.X, a.Y + b.Y, a.Z + b.Z}
}
func (a Vector3) Subtract(b Vector3) Vector3 {
return Vector3{a.X - b.X, a.Y - b.Y, a.Z - b.Z}
}
func (a Vector3) MultiplyByConstant(by float64) Vector3 {
return Vector3{a.X * by, a.Y * by, a.Z * by}
}
func (a Vector3) MultiplyByVector(by Vector3) Vector3 {
return Vector3{a.X * by.X, a.Y * by.Y, a.Z * by.Z}
}
func (a Vector3) DivideByConstant(by float64) Vector3 {
return Vector3{a.X / by, a.Y / by, a.Z / by}
}
func (a Vector3) DivideByVector(by Vector3) Vector3 {
return Vector3{a.X / by.X, a.Y / by.Y, a.Z / by.Z}
}
func (a Vector3) Length() float64 {
return math.Sqrt(a.Dot(a))
}
func (a Vector3) Normalise() Vector3 {
return a.DivideByConstant(a.Length())
}
func (a Vector3) Cross(b Vector3) Vector3 {
return Vector3{
(a.Y*b.Z) - (a.Z*b.Y),
(a.Z*b.X) - (a.X*b.Z),
(a.X*b.Y) - (a.Y*b.X),
}
}
func (a Vector3) Dot(b Vector3) float64 {
return (a.X*b.X)+(a.Y*b.Y)+(a.Z*b.Z)
}
func (a Vector3) Lerp(b Vector3, amt float64) Vector3 {
return a.MultiplyByConstant(1 - amt).Add(b.MultiplyByConstant(amt))
}
Implementing things like normalise turned up need for some other vector operations allowing division and getting the length of a vector, so I also added some tests for those:
func TestVector3_DivideByConstant(t *testing.T) {
testVector(Vector3{0.5,0,0}, UnitX().DivideByConstant(2.0), t)
}
func TestVector3_DivideByVector(t *testing.T) {
testVector(Vector3{0.5,0,0}, UnitX().DivideByVector(Vector3{2.0, 1.0, 1.0}), t)
}
func TestVector3_Length(t *testing.T) {
val := Vector3{1, 2, 3}.Length()
expected := math.Sqrt(14)
if val != expected {
t.Errorf("Length expected %f got %f", expected, val)
}
}Overall this is a concise library which is implemented in terms of itself - I'm seeing the merits of not going out and grabbing frameworks for every trivial problem, as I'd probably have spent the same amount of time researching the best vector math framework as I would have just implementing my own.
Now I can do vector operations, I can start building the raycaster, starting by getting the render direction.
Get Render Direction
Transrender's render directions are the result of a lot of careful tuning adjusting both sprite sizes and vertical angle until the output worked for OpenTTD. I can save doing all that work again by using the values as the basis for my tests. This highlights a problem though - while I could get away without having to deal with floating point rounding issues by carefully choosing my test values for the vector library, comparing between the 32-bit float values from my C# implementation and the 64-bit Go one is going to throw strict equality out of the window.
So first I need a new method in my vector library to test with an epsilon value. Test first:
func TestVector3_Equal(t *testing.T) {
testCases := []struct {
a Vector3
b Vector3
expected bool
}{
{ UnitX(), UnitX(), true },
{ UnitX(), UnitY(), false },
{ UnitX(), UnitX().Add(UnitX().MultiplyByConstant(1e-14)), true},
{ UnitX(), UnitX().Add(UnitX().MultiplyByConstant(1e-7)), false},
}
for _, testCase := range testCases {
if result := testCase.a.Equals(testCase.b); result != testCase.expected {
t.Errorf("%v == %v expected %v, was %v", testCase.a, testCase.b, testCase.expected, result)
}
}
}And then the implementation, again using the rest of the library to keep things simple and short:
func (a Vector3) Equals(b Vector3) bool {
const epsilon = 1e-14
return a.Subtract(b).Length() < epsilon
}I can now write my tests in the raycaster package for getRenderDirection:
func TestGetRenderDirection(t *testing.T) {
testCases := []struct {
angle int
expected vector3.Vector3
}{
{0, vector3.Vector3{X: -0.8944272, Z: 0.4472136}},
{45, vector3.Vector3{X: -0.6324555, Y: 0.6324555, Z: 0.4472136}},
{90, vector3.Vector3{Y: 0.8944272, Z: 0.4472136}},
}
for _, testCase := range testCases {
if result := getRenderDirection(testCase.angle); !result.Equals(testCase.expected) {
t.Errorf("Angle %d expected render direction %v, got %v", testCase.angle, testCase.expected, result)
}
}
}I can now implement the function, which turns out to be very simple:
func getRenderDirection(angle int) vector3.Vector3 {
x, y, z := -math.Cos(degToRad(angle)), math.Sin(degToRad(angle)), math.Sin(degToRad(30))
return vector3.Vector3{X: x, Y: y, Z: z}.Normalise()
}
func degToRad(angle int) float64 {
return (float64(angle) / 180.0) * math.Pi
}As expected my float64 maths returns more precise values than the C# version, so after checking they still make sense I substitute those into my test and everything is good.
For now I'm happy not testing the degToRad function separately, the unit is getting the render direction and I'm not interested in constraining internal details of how it converts angles. (As an unlikely example, if math.Cos turned out to be a bottleneck I might end up using a lookup table, in which case the integer angle would be fine).
Get Viewport Plane
Taking this unit-level philosophy, the next thing I need is the viewport plane. We could test the steps to build this up (getting the render normal and viewpoint) but I think this will be simple enough there's not a large amount of value testing at that level. As creating structures is low-friction in Go (and nobody's going to complain that I should have made a class instead) I add a plane to the raycaster package:
type plane struct {
A, B, C, D vector3.Vector3
}Right now this feels a reasonable place to put it, 3D planes are not used anywhere else and I use a lowercase name so it doesn't get exported. With this in place and using the same approach of taking the values from the C# version, I end up with this as my test:
func TestGetViewportPlane(t *testing.T) {
testCases := []struct {
angle int
expected plane
}{
{0, plane{
vector3.Vector3{X: -26.44272, Y: -43, Z: 127.7214},
vector3.Vector3{X: -26.44272, Y: 83, Z: 127.7214},
vector3.Vector3{X: -26.44272, Y: 83, Z: 1.721359},
vector3.Vector3{X: -26.44272, Y: -43, Z: 1.721359},
}},
{45, plane{
vector3.Vector3{X: -44.79328, Y: 38.69782, Z: 127.7214},
vector3.Vector3{X: 44.30218, Y: 127.7933, Z: 127.7214},
vector3.Vector3{X: 44.30218, Y: 127.7933, Z: 1.721359},
vector3.Vector3{X: -44.79328, Y: 38.69782, Z: 1.721359},
}},
{90, plane{
vector3.Vector3{Y: 109.4427, Z: 127.7214},
vector3.Vector3{X: 126, Y: 109.4427, Z: 127.7214},
vector3.Vector3{X: 126, Y: 109.4427, Z: 1.721359},
vector3.Vector3{Y: 109.4427, Z: 1.721359},
}},
}
for _, testCase := range testCases {
if result := getViewportPlane(testCase.angle); !result.Equals(testCase.expected) {
t.Errorf("Angle %d expected viewport plane %v, got %v", testCase.angle, testCase.expected, result)
}
}
}Almost immediately I'm noticing that a plane.Equals() method would be useful. I don't want to start filling up my raycaster with lots of details about how to compare planes, though. So I'm going to override my earlier decision - while planes might not be used anywhere else, they do have their own concerns which are unrelated to raycasting.
One thing Go newbies like me apparently suffer from is package-itis, where every minor concern is its own package and the whole thing becomes an enormous mess. However I can already see a solution to this - if my vector3 package becomes a more generic geometry package, planes will naturally fit in there.
What used to be my vector directory now looks like this:
I can now write a test for Equals:
func TestPlane_Equals(t *testing.T) {
plane1 := Plane{A: Vector3{Y: 1}, B: Vector3{X: 1, Y: 1}, C: Vector3{X: 1}, D: Vector3{}}
plane2 := Plane{A: Vector3{Y: 2}, B: Vector3{X: 1, Y: 2}, C: Vector3{X: 1}, D: Vector3{}}
testCases := []struct {
a Plane
b Plane
expected bool
}{
{plane1, plane1, true},
{plane2, plane2, true},
{plane1, plane2, false},
}
for _, testCase := range testCases {
if result := testCase.a.Equals(testCase.b); result != testCase.expected {
t.Errorf("%v == %v expected %v, was %v", testCase.a, testCase.b, testCase.expected, result)
}
}
}
And then the implementation, which is a lot simpler as I'm just reusing the vector .Equals for all four corners:
func (a Plane) Equals(b Plane) bool {
return a.A.Equals(b.A) && a.B.Equals(b.B) && a.C.Equals(b.C) && a.D.Equals(b.D)
}Now we have the red test for the raycaster's getViewportPlane to deal with, so let's get back to implementing that.
One shortcoming of C# Transrender is it expects all voxel objects to be 126x40xsomething in size, and you'll get unexpected results if that's not the case. I don't want to change the behaviour around height because it allows for some details in sprites to be taller than an OpenTTD sprite is allowed to be, like tram poles, without the renderer squashing the whole sprite to try to make it fit.
However it would be nice if GoRender handles sprites of different size. So I'm going to add parameters for the x and y dimensions, with the assumption height should scale the same as width.
The resulting function looks like this:
func getViewportPlane(angle int, x int, y int) geometry.Plane {
midpoint := geometry.Vector3{X: float64(x) / 2.0, Y: float64(y) / 2.0, Z: float64(y) / 2.0}
viewpoint := midpoint.Add(getRenderDirection(angle).MultiplyByConstant(100.0))
planeNormal := geometry.UnitZ().MultiplyByConstant(midpoint.X)
renderNormal := getRenderNormal(angle).MultiplyByConstant(midpoint.X)
a := viewpoint.Subtract(renderNormal).Add(planeNormal)
b := viewpoint.Add(renderNormal).Add(planeNormal)
c := viewpoint.Add(renderNormal).Subtract(planeNormal)
d := viewpoint.Subtract(renderNormal).Subtract(planeNormal)
return geometry.Plane{A: a, B: b, C: c, D: d}
}
func getRenderNormal(angle int) geometry.Vector3 {
x, y := -math.Cos(degToRad(angle)), math.Sin(degToRad(angle))
return geometry.Vector3{X: y, Y: -x}.Normalise()
}Updating the test to send 126 and 40 for x and y respectively (the values hard-coded into the C# version) gives results within 0.00001 of my expected test values, so I feel happy enough to copy these back into the test and everything is now green.
Interpolate ray starting point
My code is looking a lot cleaner than the C# version, and I only have one ray initialisation step left: interpolate the starting positions across the plane using the u and v co-ordinates of the render target. Given this is more of a plane concern than a raycaster one, I can put the logic in the geometry package as the somewhat clunkily-named BiLerpWithinPlane function.
The test looks like this:
func TestPlane_BiLerpWithinPlane(t *testing.T) {
plane := Plane{A: Vector3{Y: 2}, B: Vector3{X: 2, Y: 2}, C: Vector3{X: 2}, D: Vector3{}}
testCases := []struct {
p Plane
u, v float64
expected Vector3
}{
{plane, 0, 0, Vector3{Y: 2}},
{plane, 1, 0, Vector3{X: 2, Y:2}},
{plane, 0, 1, Vector3{}},
{plane, 1, 1, Vector3{X: 2}},
{plane, 0.5, 0.5, Vector3{X: 1, Y: 1}},
}
for _, testCase := range testCases {
if result := testCase.p.BiLerpWithinPlane(testCase.u, testCase.v); result != testCase.expected {
t.Errorf("Bilerp %v with [%f,%f] expected %v, was %v", testCase.p, testCase.u, testCase.v, testCase.expected, result)
}
}
}Implementing it is a simple case of using our existing Vector3.Lerp() function:
func (a Plane) BiLerpWithinPlane(u float64, v float64) Vector3 {
abu, dcu := a.A.Lerp(a.B, u), a.D.Lerp(a.C, u)
return abu.Lerp(dcu, v)
}This could be a single-liner given all these functions can be chained, but I think I'm already up against the limit of readability so this is likely to be more maintainable.
C# Transrender also has an optimisation where the ray gets set to the point where it intersects the bounding volume before getting stepped for the first time, but if all we care about is "working" this can be ignored - performance optimisation can come later when I need it.
Raycasting: inside/outside tests
The raycaster has two important tests which we need to implement next:
- If the ray is currently inside the bounding volume
- If the ray is outside the bounding volume and will not intersect it in future
The C# naming is not quite perfect (why does IsOutside() != IsInsideObject() for some cases?) so I'm going to rename these to isInsideBoundingVolume() and canTerminateRay() to make it clearer what they're used for.
Another problem with the C# version is it uses module-level variables so isn't very testable. That's another thing to fix. With this in mind, my function signature are going to look like this:
func isInsideBoundingVolume(loc geometry.Vector3, limits geometry.Vector3) bool {
}
func canTerminateRay(loc geometry.Vector3, ray geometry.Vector3, limits geometry.Vector3) bool {
}As the raycasting is currently done in the floating point domain, I'm going to request the limits as a Vector3 so these functions (which will be used in a tight loop) aren't constantly converting integers to floating point. Long term I might switch to a DDA-based raycaster in the integer domain to avoid the potential for rays to "slip" between voxels in the grid, but I can refactor this when I get there.
The tests for these methods are:
func TestIsInsideBoundingVolume(t *testing.T) {
testCases := []struct {
loc, limits geometry.Vector3
expected bool
}{
{geometry.Vector3{}, geometry.Vector3{X: 2, Y: 2, Z: 2}, true},
{geometry.Vector3{X: 1, Y: 1, Z: 1}, geometry.Vector3{X: 2, Y: 2, Z: 2}, true},
{geometry.Vector3{X: 4, Y: 2, Z: 2}, geometry.Vector3{X: 2, Y: 2, Z: 2}, false},
{geometry.Vector3{X: -1, Y: 2, Z: 2}, geometry.Vector3{X: 2, Y: 2, Z: 2}, false},
}
for _, testCase := range testCases {
if result := isInsideBoundingVolume(testCase.loc, testCase.limits); result != testCase.expected {
t.Errorf("co-ordinates %v inside %v expected %v, got %v", testCase.loc, testCase.limits, testCase.expected, result)
}
}
}
func TestCanTerminateRay(t *testing.T) {
testCases := []struct {
loc, ray, limits geometry.Vector3
expected bool
}{
{geometry.Vector3{X: 1}, geometry.Vector3{X: 1}, geometry.Vector3{X: 2, Y: 2, Z: 2}, false},
{geometry.Vector3{X: 1}, geometry.Vector3{X: -1}, geometry.Vector3{X: 2, Y: 2, Z: 2}, false},
{geometry.Vector3{X: -1}, geometry.Vector3{X: 1}, geometry.Vector3{X: 2, Y: 2, Z: 2}, false},
{geometry.Vector3{X: -1}, geometry.Vector3{X: -1}, geometry.Vector3{X: 2, Y: 2, Z: 2}, true},
{geometry.Vector3{X: 3}, geometry.Vector3{X: 1}, geometry.Vector3{X: 2, Y: 2, Z: 2}, true},
{geometry.Vector3{X: 3}, geometry.Vector3{X: -1}, geometry.Vector3{X: 2, Y: 2, Z: 2}, false},
}
for _, testCase := range testCases {
if result := canTerminateRay(testCase.loc, testCase.ray, testCase.limits); result != testCase.expected {
t.Errorf("co-ordinates %v can terminate ray %v for limits %v expected %v, got %v", testCase.loc, testCase.ray, testCase.limits, testCase.expected, result)
}
}
}
As with a lot of these tests they're kinda boilerplate-y, but since most of that is data I'm not sure how much we'd gain from the C#/Java style of annotated test methods, other than not having to do that range iterator each time.
Again the implementation is simple, there's no reason to change anything much from the C# implementation once the naming has been sorted out:
func isInsideBoundingVolume(loc geometry.Vector3, limits geometry.Vector3) bool {
return loc.X >= 0 && loc.Y >= 0 && loc.Z >= 0 && loc.X < limits.X && loc.Y < limits.Y && loc.Z < limits.Z
}
func canTerminateRay(loc geometry.Vector3, ray geometry.Vector3, limits geometry.Vector3) bool {
return (loc.X < 0 && ray.X <= 0) || (loc.Y < 0 && ray.Y <= 0) || (loc.Z < 0 && ray.Z <= 0) ||
(loc.X > limits.X && ray.X >= 0) || (loc.Y > limits.Y && ray.Y >= 0) || (loc.Z > limits.Z && ray.Z >= 0)
}Tests are green and we can start thinking about raycasting something.
Casting rays
I now have an interesting problem, which is that I don't really know what I want to test for the raycaster output. Or rather, I do know what the output should look like on a conceptual level but trying to write tests for that before I see it will be slow, painful and involve a lot of working things out on paper.
This might be a good argument to use a more end-to-end test where I provide a .vox file and a .png file of what I expect, or possibly to figure out a really constrained raycasting problem, but right now I want to keep momentum so I'm going to drop to iterate-and-stabilise mode. C# Transrender suggests that bad things happen if that's used for a whole project, but the raycaster is a relatively constrained part and as I write it I may discover things I can make testable.
I know from the C# version that the raycaster output is actually a composite of colour information, lighting information and maybe some other things that haven't been explored like depth. So I don't want my raycaster to output an image directly; turning this into an image should be the responsibility of the sprite package.
I'm going to introduce some types for the raycaster output:
type RenderInfo struct {
Collision bool
}
type RenderOutput [][]RenderInfoCurrently we just track whether we collided with a voxel at this location or not. One nice thing here is I can extend this without breaking anything used in sprite, which will help me extract testable parts after this phase of exploratory coding.
I feel like I know enough to decide on the function signature, so I'm going to start with taking in a voxel object, an angle, and width/height of the render target.
func GetRaycastOutput(object voxelobject.RawVoxelObject, angle int, w int, h int) RenderOutput {
}The first problem here is it'd be nice to know how big RawVoxelObject is. So I'm going to add a function to voxelobject before going any further. There's nothing too complicated here. Test:
func TestRawVoxelObject_Size(t *testing.T) {
size := Point{X: 1, Y: 2, Z: 3}
object := MakeRawVoxelObject(size)
if object.Size() != size {
t.Errorf("expected size %v but was %v", size, object.Size())
}
}Implementation:
func (o RawVoxelObject) Size() Point {
return Point{
X: byte(len(o)),
Y: byte(len(o[0])),
Z: byte(len(o[0][0])),
}
}I also take this opportunity to move the initialisation of an empty RawVoxelObject from the vox package to voxelobject, as it's now feeling more like a concern of the raw object itself than the format-specific reader.
Back to getRaycastOutput and I can now set up the limits which I'll use for my inside bounding box and ray termination tests:
size := object.Size()
limits := geometry.Vector3{X: float64(size.X), Y: float64(size.Y), Z: float64(size.Z)}Next we can set up the viewport and ray:
viewport := getViewportPlane(angle, size.X, size.Y)
ray := geometry.Zero().Subtract(getRenderDirection(angle))This elicits a quick refactor as it now makes life easier for getViewportPlane to accept byte as the type for its sizes. Note I also follow the C# Transrender convention where renderDirection is the ray outward from the object, and we negate it when rendering.
Now it's time to write the core of the raycaster!
result := make(RenderOutput, w)
for x := 0; x < w; x++ {
result[x] = make([]RenderInfo, h)
for y := 0; y < h; y++ {
u, v := float64(x) / float64(w), float64(y) / float64(h)
loc := viewport.BiLerpWithinPlane(u, v)
for {
if canTerminateRay(loc, ray, limits) {
break
}
if isInsideBoundingVolume(loc, limits) {
lx, ly, lz := byte(loc.X), byte(loc.Y), byte(loc.Z)
if object[lx][ly][lz] != 0 {
result[x][y].Collision = true
}
}
loc = loc.Add(ray)
}
}
}This is straight out of the C# version. We set up the RenderInfo structure for each location, then set the location (loc) to its starting point. From that point we check if we can terminate it and exit the loop if so. Otherwise if we're inside the bounding volume we see if there is a voxel at this location. If there is we set Collision to true.
Finally we increment the ray using floating point vector addition. This isn't totally accurate but produced "good enough" results in the C# version so let's keep it for now.
I'm now in a situation where I have code, but no tests and nothing using it. So first I go to my sprite package and update that. I rename our existing GetSprite method to GetUniformSprite so it's still available for tests which don't want the complication of guessing what the raycast renderer is going to output. Then I add GetRaycastSprite:
func GetRaycastSprite(object voxelobject.RawVoxelObject, bounds image.Rectangle, angle int) image.Image {
info := raycaster.GetRaycastOutput(object, angle, bounds.Max.X, bounds.Max.Y)
img := image.NewRGBA(bounds)
for x := bounds.Min.X; x < bounds.Max.X; x++ {
for y := bounds.Min.Y; y < bounds.Max.Y; y++ {
if info[x][y].Collision {
img.Set(x, y, color.Black)
} else {
img.Set(x, y, color.White)
}
}
}
return img
}I break a couple of tests and getting back to green involves adding some error handling and a little bit of clunky logic in GetSpritesheets to use GetUniformSprite if it's passed an empty object, and the raycaster otherwise.
I now update my increasingly unwieldy main package:
func main() {
if len(os.Args) < 2 {
s := fmt.Sprintf("no command line argument given for voxel file source")
panic(s)
}
voxFile, err := os.Open(os.Args[1])
if err != nil {
s := fmt.Sprintf("could not open input file: %s", err)
panic(s)
}
object, err := vox.GetRawVoxels(voxFile)
if err != nil {
s := fmt.Sprintf("could not read voxel file: %s", err)
panic(s)
}
if err := voxFile.Close(); err != nil {
s := fmt.Sprintf("error closing voxel file: %s", err)
panic(s)
}
sheets := spritesheet.GetSpritesheets(object, 1.0, 8)
sheet, ok := sheets["32bpp"]
if !ok {
panic("no 32bpp sprite sheet available")
}
imgFile, err := os.Create("output.png")
if err != nil {
s := fmt.Sprintf("could not open output image file: %s", err)
panic(s)
}
if err := png.Encode(imgFile, sheet.Image); err != nil {
imgFile.Close()
s := fmt.Sprintf("error writing image file: %s", err)
panic(s)
}
if err := imgFile.Close(); err != nil {
s := fmt.Sprintf("error closing image file: %s", err)
panic(s)
}
}Yech! This works for now but it looks horrible, like one of my QBASIC programs from the early '90s. Cleaning this up is going to be a priority once we get to our desired MVP state.
Contact with the real world also highlights another bug - the size in MagicaVoxel files isn't an int64, it's actually an int32 with the size in bytes of the main chunk followed by an int32 with the size in bytes of the child chunks. Cautionary lesson to read the documentation!
We also miss that there's a version identifier after the file magic, which can be worked around for now by treating it as another 4-character chunk identifier. With both those problems sorted and tests updated to reflect the changes in behaviour, there's only one thing left to do:
D:\projects\gorender\src>go build cmd/renderobject && renderobject.exe bus.vox
D:\projects\gorender\src>
This produces a new version of output.png... and opening it reveals that I managed to do what I wanted:
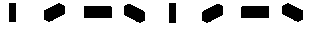
It feels like we're very close to producing a flat-shaded sprite, but this is is understating the task of loading the Transport Tycoon palette and processing it in our raycaster.
A part 4 beckons...
